Scratchcards are played by millions of people every day, with only a lucky few who strike gold and walk away an instant millionaire.
But are they really “lucky”?
What if there was a way to improve your chances of winning, or cheat the system?
Well, one man argues that scratchcards aren’t actually random and even has a system to prove it: The Singleton Method.
Let’s take a look how he discovered the popular Singleton Method, how it works, and whether or not scratchcard manufacturers have done anything about it.
In 2003, a geological statistician living in Toronto named Mohan Srivastava was waiting for some files to download on his computer. To pass the time, he decided to play some old scratch cards that were lying around.
He lost the first one but won a small amount of cash on a tic-tac-toe scratch card. It was this win that got him thinking about how they’re made.
What initially started as an interest about the computer’s algorithm led to him effectively cracking the code of scratch cards.
Knowing that the tickets were mass-produced, he figured that they couldn’t be totally random since the manufacturers needed to control the number of winning tickets.
After a bit of research and ticket buying, he discovered a flaw in the way scratchcards are made. Once he’d worked it out, he was able to devise a method to cheat them.
You might be expecting a highly complex system, that only those with years of education at MIT would understand. This isn’t the case though.
Instead, Srivastava’s method simply relies on looking to see which numbers are visible on a card before it’s bought. You don’t need to scratch anything off, you just need to look at the numbers that are visible on the side, as they actually reveal essential information.
He found that if a number on the side appeared only once, then it would almost always appear under the latex coating that needed to be scratched off.
He was looking for singletons.
The below graphic by Toronto Star shows how his method works:
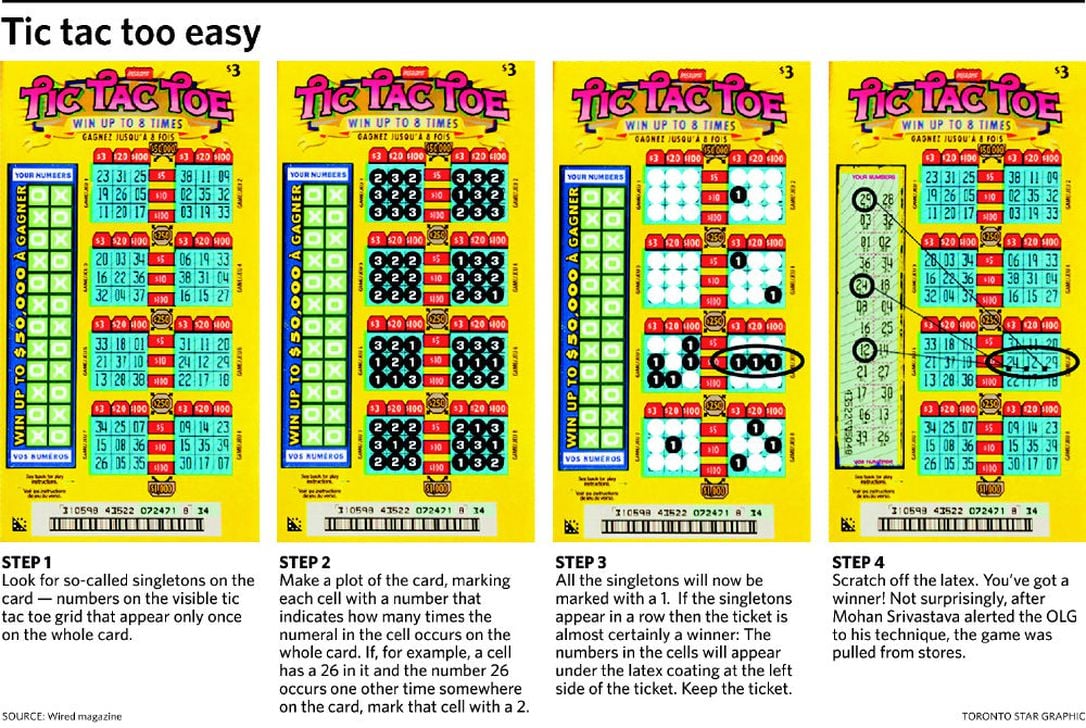 All you need to do is look out for those all-important singletons.
All you need to do is look out for those all-important singletons.
[Image: Toronto Star]
So, as you can see, it was easy: those looking to win just needed to find cards that had a few single numbers on them. Cards with three singletons on the same row were pretty much always a winning ticket.
While this didn’t guarantee a prize, it made the odds of winning much higher.
In fact, Srivastava found that tickets he selected had a 90 percent of chance of being winners.
While Srivastava reported his findings to the Ontario Lottery and Gaming Corporation, causing the tic-tac-toe game he studied to be pulled, they stated that it was simply caused by a design flaw in the game.
But this wasn’t just a trick Srivastava could use on a single type of scratchcard, it was a method that could be used all over.
This is because most scratchcards in North America are produced by just a few companies, so the bad practice extended to other scratchcards as well. Therefore, Srivastava’s trick could be used to crack most scratchcards on the continent.
He continued to test his method with other similar scratch lottery games.
Srivastava would later have tickets sent to him from Colorado, and he found that the same patterns were evident. He would also buy more scratchcards in Toronto and once again discover the issue was still there.
Clearly the companies producing the tickets hadn’t learned from the information he had provided them with.
But why haven’t they done anything about it?
According to Srivastava, it’s because they can’t.
This is because while the producers want everyone to think that scratchcards are a game of chance, it’s almost impossible to make them truly random.
Companies use algorithms to ensure the correct number of winning cards are produced. If they didn’t then they couldn’t control the number of winning tickets.
But it’s these algorithms that give a way in for those clever enough to exploit them, such as Srivastava.
As yet, it doesn’t seem like the flaw has been fixed by scratchcard companies. In fact, as we previously explained, it might be the case that the flaw can’t be fixed.
If you want to use it, you should know that the Singleton Method only works on extended play scratchcards, where you scratch off numbers and match them with numbers already shown. This is because these visible numbers are the key to this system.
Another thing to note is that you need to be able to see the fronts of scratchcards before you buy them, which isn’t always possible.
On top of this, there’s no guaranteeing how much you’ll win, so you could go to the effort of identifying and purchasing a winner, only to find that you’ve only won $2.
Srivastava did the math and didn’t think it was worth his time or money. But could you scale the process to make it worthwhile for you?
Overall, however, it is still possible for this system to be used, providing the situation is right.
Why not try it the next time you head to the store to buy one?